Tower of Hanoi Algorithm | Tower of Hanoi problem in Data Structure | Tower of Hanoi Recursive Solution | Tower of Hanoi C++

🧠 1. What is Backtracking?

Backtracking is a problem-solving technique used to build up a solution incrementally and remove those solutions that fail to meet the problem constraints (i.e., “backtrack”).

Backtracking is like trying all possibilities, but avoiding wrong paths early.

🔑 Key Idea:

Try → If it fails → Undo → Try next option.

Imagine a maze:

• You go forward…
• If you hit a wall (wrong path), you backtrack (go back) to the previous step.
• Then try another path.

Backtracking is:

Try → Check → If invalid → Undo → Try next

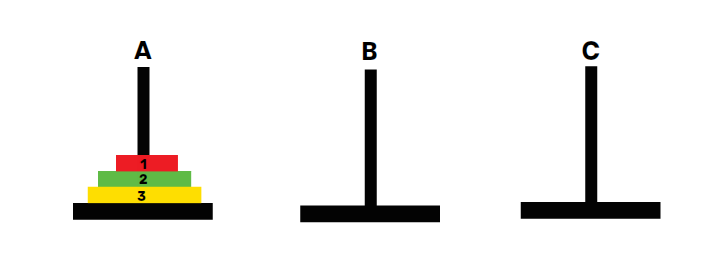
🗼 2. Tower of Hanoi

Tower of Hanoi is a classic recursion and backtracking example.

🧩 Problem Statement:

• You have 3 rods and n disks.
• Move all disks from Source (A) to Destination (C) using an Auxiliary (B) rod.
• Rules:
  1. Only one disk can be moved at a time.
  2. A larger disk cannot be placed on top of a smaller disk.

✅ C++ Implementation

#include <iostream>
using namespace std;

void towerOfHanoi(int n, char from_rod, char to_rod, char aux_rod) 
{
    if (n == 1) 
    {
        cout << "Move disk 1 from rod " << from_rod << " to rod " << to_rod  << endl;
        return;
    }

    // Move top n-1 disks from source to auxiliary
    towerOfHanoi(n - 1, from_rod, aux_rod, to_rod);

    // Move remaining disk to destination
    cout << "Move disk " << n << " from rod " << from_rod << " to rod " << to_rod << endl;

    // Move n-1 disks from auxiliary to destination
    towerOfHanoi(n - 1, aux_rod, to_rod, from_rod);
}

int main() 
{
    int n = 3; // Number of disks
    towerOfHanoi(n, 'A', 'C', 'B');  // A = source, C = destination, B = auxiliary
    return 0;
}

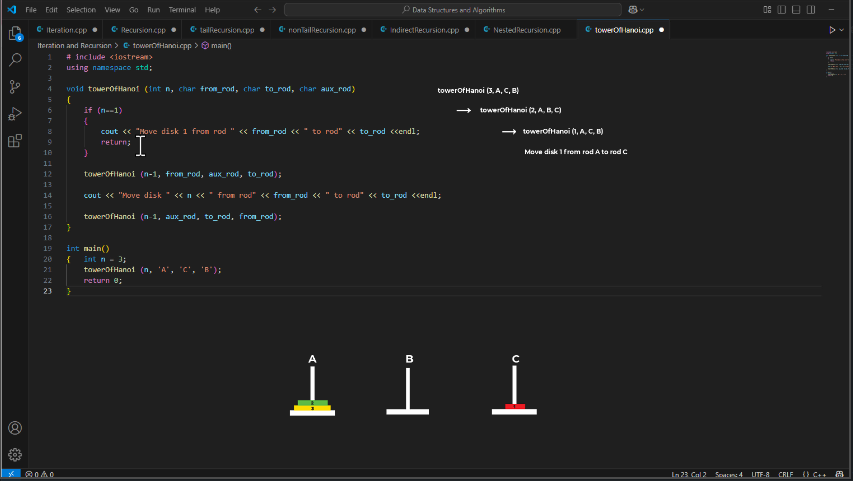
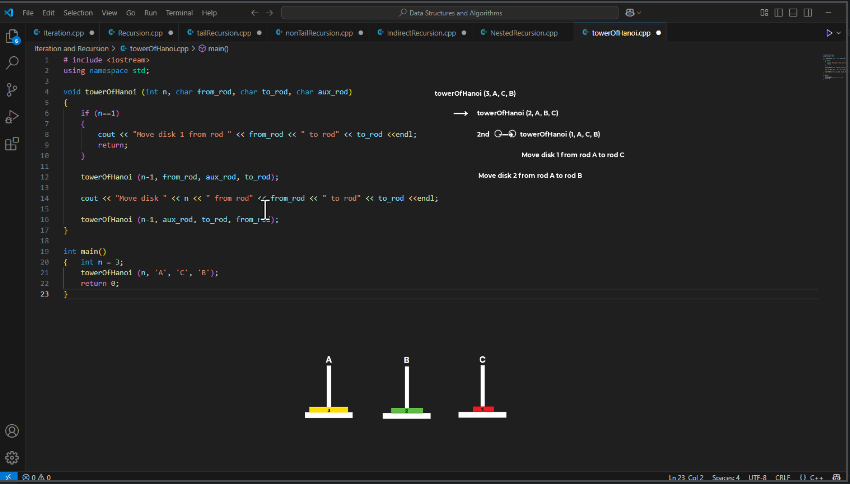
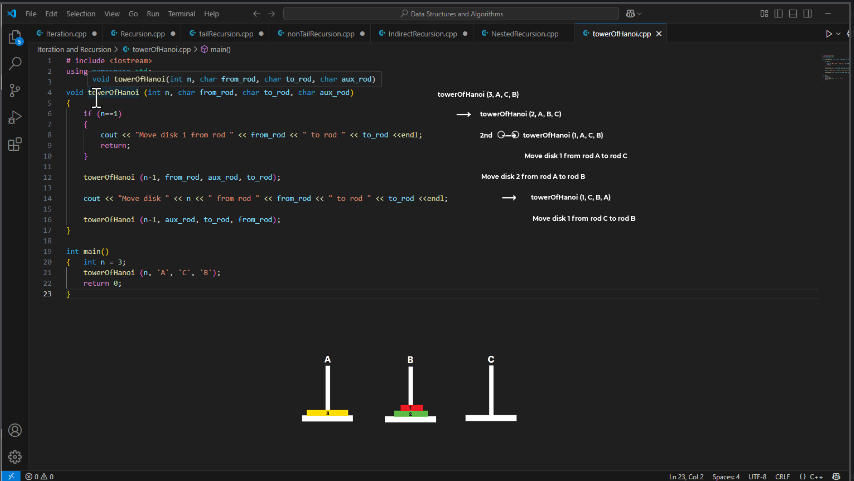
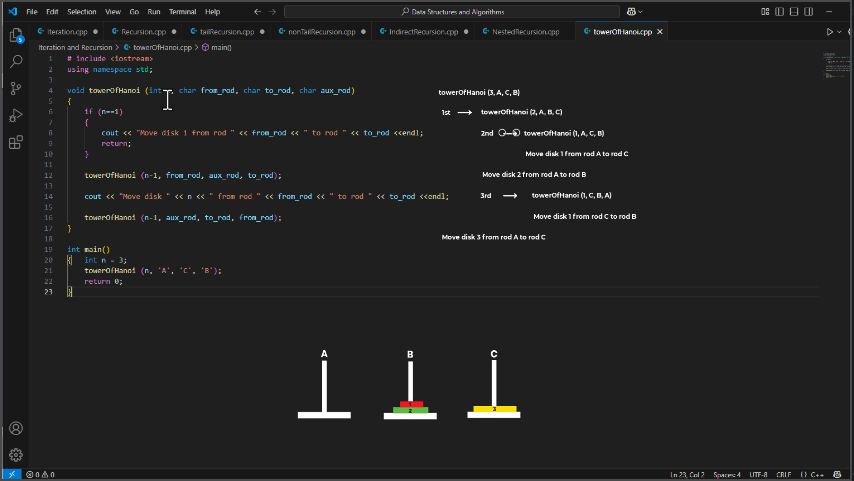
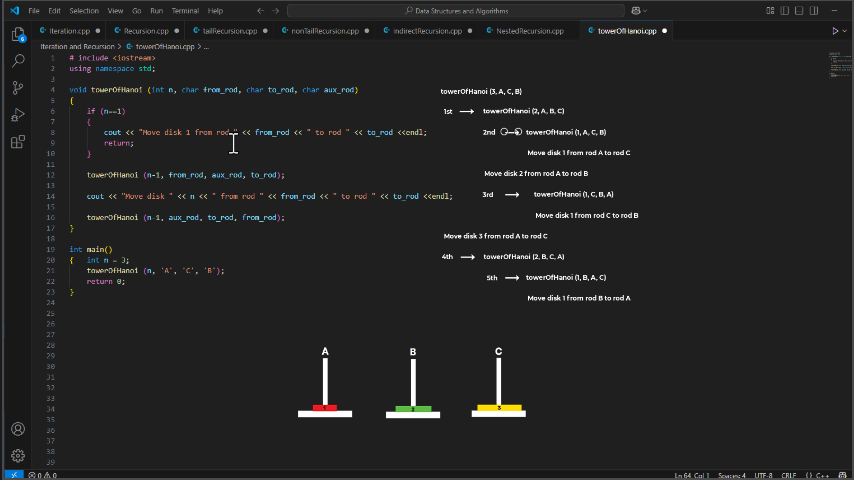
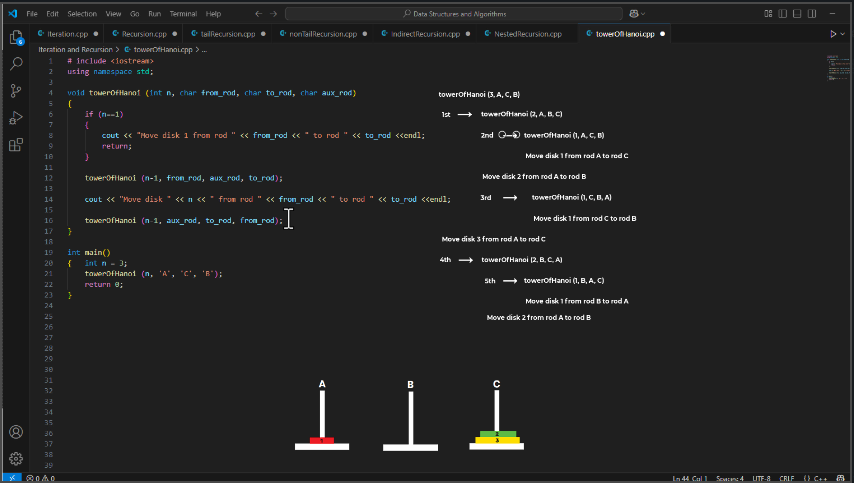
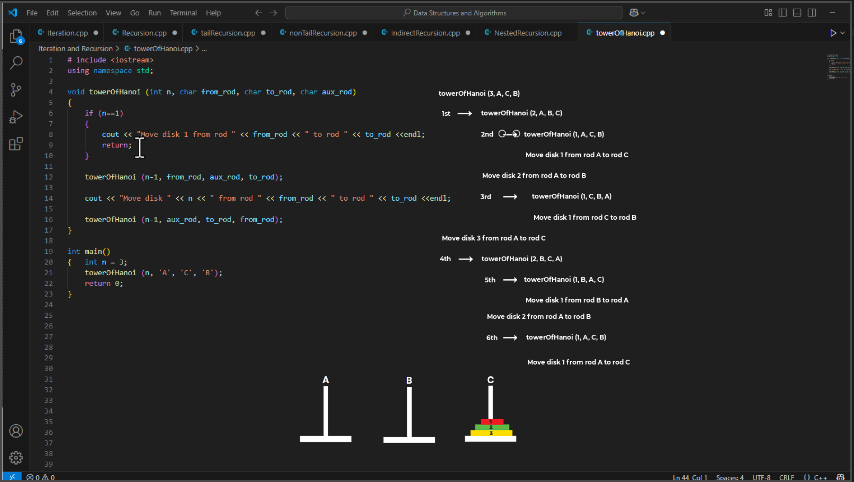
🧾 Output for n = 3:

cssCopyEditMove disk 1 from rod A to rod C
Move disk 2 from rod A to rod B
Move disk 1 from rod C to rod B
Move disk 3 from rod A to rod C
Move disk 1 from rod B to rod A
Move disk 2 from rod B to rod C
Move disk 1 from rod A to rod C

🔁 How It’s Backtracking:

• It tries moving smaller disks first.
• Then comes back (“backtracks”) to move the larger ones when allowed.
• Follows all constraints by carefully undoing and redoing moves as needed.

“How does Tower of Hanoi use backtracking?”

Let’s break that down.

📌 Tower of Hanoi Rules:

1. Move all disks from Rod A to Rod C.
2. Only one disk can move at a time.
3. A larger disk can’t be placed on a smaller one.

💡 Backtracking in Action:

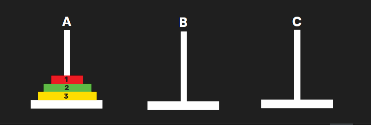
Let’s say you have 3 disks on rod A: Disk 3 (bottom), 2, 1 (top).

You want to move them to rod C.

Here’s the step-by-step backtracking-like logic:

🔁 Step 1: Try Moving Smaller First

• You can’t move disk 3 first — it’s at the bottom.
• So, the algorithm tries to move the top 2 disks first (recursive step).

🔙 Step 2: Move Disk 1 → Allowed ✅

• Move Disk 1 from A → C.

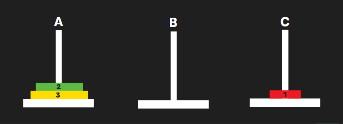
🔁 Step 3: Try to Move Disk 2 → Needs Free Rod

• Move Disk 2 from A → B.

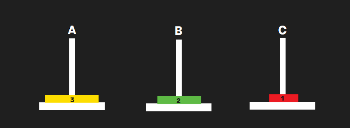
🔁 Step 4: Now, Disk 1 is blocking → Must Move It

• Move Disk 1 from C → B to make space for disk 3.

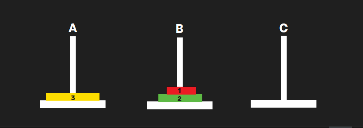
➡️ This is where backtracking happens:

• You’re undoing a previous move (moving disk 1 again) to make space for a new move.

🔁 Step 5: Move Disk 3 → A to C ✅

• Finally, you can move the biggest disk.

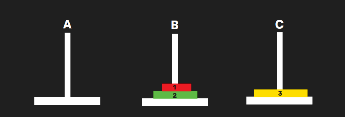
🔁 Step 6: Restore Earlier Smaller Disks

• Now you move disk 1 and 2 again on top of disk 3.

➡️ You’re repeating/redoing earlier steps in a new way (that’s also backtracking).

✅ How It’s Backtracking:

Concept	Tower of Hanoi Example
Try	Try moving top disks first
If Blocked	You can’t move large disk → go move smaller first
Undo	Move small disk back to make room (e.g., 1 → C → B)
Try Again	Now try moving the bigger disk

🧠 Backtracking is like:

“I can’t do this move right now, so let me go back, fix the situation, and try again — step by step.”