Prefix to Infix conversion using stack – DSA Course Playlist in C++ – Coding With Clicks

✅ Prefix to Infix Conversion

💡 Rules:

Scan the prefix expression right to left.
If the token is an operand, push it to the stack.
If the token is an operator, pop two operands from the stack.
Combine them as:
(<operand1> <operator> <operand2>)
Push the resulting string back to the stack.
Final result on the stack is the infix expression.

🧠 Example:

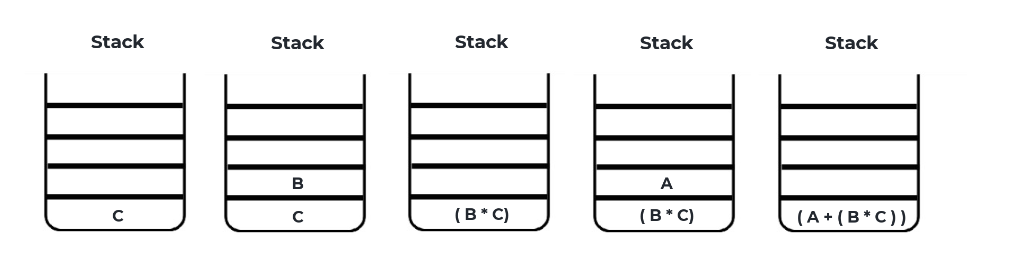
Prefix: + A * B C

Steps:

Read C → push
Read B → push
Read * → pop B and C → (B * C) → push
Read A → push
Read + → pop A and (B * C) → (A + (B * C))

✅ Infix: (A + (B * C))

when we say “push the result back to the stack,” like "(B * C)", we’re treating the entire expression as a single operand-like unit, but only in terms of stack processing, not as a literal operand like A, B, or C.

🔍 Let’s clarify the roles:

Real operands: Variables or constants like A, B, C.
Operators: Symbols like +, *, /, etc.
Sub-expressions like "(B * C)": These are not real operands, but during processing, we treat them as atomic units (strings) to allow nesting.

In Simple Words:

Yes — "(B * C)" is treated like an operand only for stack handling purposes, but logically, it’s a composite infix expression made of operands and operators.

🔍 Why Parentheses Are Needed in Infix

In infix notation, operator precedence matters. For example:

A + B * C means A + (B * C) because * has higher precedence than +.

But if you convert prefix + A * B C to plain infix as A + B * C — without parentheses — it’s unclear whether you meant:

(A + B) * C or
A + (B * C)

That’s why parentheses are added in the infix result, to make the expression unambiguous, regardless of operator precedence.