4. Bayesian Networks
Definition:
A Bayesian Network (also called a Belief Network) is a probabilistic graphical model. It shows how different variables (things that can change) are related through probabilities.
What does “probabilistic graphical model” mean?
It’s a combination of three ideas:
1. Probabilistic
This means it deals with uncertainty.
- It indicates the likelihood that something will occur rather than whether it is unquestionably true or not.
- Example:
- There is a 90% chance the patient has flu if they have a fever and cough.
2. Graphical
This refers to a graph structure — like a network or diagram:
- Nodes (circles) = Variables (e.g., Disease, Symptom, Malfunction).
- Arrows = Relationships (e.g., one causes or influences another).
3. Model
A model is an illustration of the real world.
- It helps us understand, predict, or reason about things in the real world.
- What does this term “model” mean?
A model is a simplified representation of reality that helps us understand, predict, or make decisions about real-world situations.
Consider it as follows:
A model is not the real thing, but a useful version of it — just enough detail to help us think or act wisely.
Real-life examples of models:
Model Type
What it Represents
Why it’s Useful
Map
Real-world geography
Helps you find directions
Weather model
Atmosphere and climate
Predicts rain, storms, temperatures
Economic model
Spending, inflation, jobs, etc.
Helps predict the economy
Bayesian Network model
Variables and their probabilities
Helps reason under uncertainty
In AI or computer science:
A model can be:
A mathematical or logical structure
That simulates how something works in the real world
And helps us make predictions or decisions
Summary:
Model = A smart shortcut for reality.
It’s something we create (with math, logic, or data) to help us understand or predict how real things behave.
- What does this term “model” mean?
Original sentence:
“It shows how different variables (things that can change) are related through probabilities.”
What does it signify?
“Different variables (things that can change)”
- These are factors or items that can take on different values.
- Example variables:
- Symptom = fever / no fever
- Disease = flu / no flu
- Component = working / malfunctioning
So “variables” are just changeable things we care about.
“Are related through probabilities”
This means:
- The variables are connected, but not with certainty.
- Instead, we use probability to describe how likely one variable affects another.
Example:
Let’s say we have two variables:
nginxCopyEditFlu → Fever
This means:
- Having flu increases the probability of having a fever.
- But not always — maybe flu causes fever 90% of the time.
They are therefore probabilistically connected but not necessarily so.
Combining everything:
A Bayesian Network shows how changeable things (variables) like diseases or symptoms are linked, not with 100% certainty, but by how likely one affects or explains another.
Why it’s useful:
It provides answers to queries such as:
“If I see a fever, what’s the chance the person has flu?”
Instead of a yes/no answer, it gives a probability, like:
“There’s a 90% chance it’s the flu.”
It provides answers to queries such as:
- “If this symptom is observed, how likely is it that the patient has this disease?”
- “If this part is malfunctioning, how likely is it to cause a system failure?”
Purpose:
Performing reasoning under uncertainty, where you don’t have all the facts but have probabilities and can use them to make educated guesses, is the primary objective of a Bayesian network.
What is “reasoning”?
Reasoning is the process of applying logic to arrive at a conclusion or decide on a course of action based on your knowledge.
In simple terms:
Reasoning = Using what you know → to figure out something you don’t know.
Example:
Let’s say:
- You know: Fever is usually caused by the flu.
- You observe: A person has a fever.
- You reason: “Maybe they have the flu.”
Even if you’re not 100% sure — you’re using what you know to make an informed guess.
That is reasoning.
In the sentence you gave:
“The main goal of a Bayesian Network is to perform reasoning under uncertainty…”
This means:
- The Bayesian Network is used to think logically (reason),
- Even when we don’t know everything,
- By using probabilities to guess what is most likely.
Summary:
| Term | Meaning |
|---|---|
| Reasoning | Thinking logically to reach conclusions |
| Under uncertainty | Even when you’re not 100% sure |
| With probabilities | Using chances/likelihoods to support your thinking |
What does “where you don’t have all the facts” mean?
It means:
You are not entirely certain of everything.
Some information is missing, uncertain, or not directly available.
In simple terms:
You’re in a situation where:
- You don’t know the full truth
- You can’t be 100% sure about what’s happening
- But you still need to make a decision or guess
Examples:
- Medical example:
- You don’t know for sure if the patient has the flu.
- But you see a cough and fever.
- So, you reason using probabilities to guess what’s likely.
- Tech example:
- A machine stops working.
- Although you have data indicating which parts fail most frequently, you are unsure of the precise part that is broken.
- You make an informed guess based on that.
In the full sentence:
“Reasoning under uncertainty — where you don’t have all the facts…”
It means:
- You’re not in a perfect world with full knowledge.
- You’re using probabilities and logic to figure things out anyway.
Summary:
| Phrase | Meaning |
|---|---|
| You don’t have all the facts | You lack full information; things are unclear or unknown |
| Still using reasoning | You think smartly with what you do know |
How it Works:
1. Graph Structure:
- Every node in the graph is a variable (e.g., Fever, Disease, EmailType).
- Directed arrows between nodes represent dependencies or causal relationships.
- For example, an arrow from Disease → Fever means “having a disease can cause fever.”
2. Probabilities:
Each node has a Conditional Probability Table (CPT) that shows how likely it is given its parent(s).
What does this part mean?
“How likely it is given its parent(s)”
Step-by-step explanation:
1. “It” = the current node (or variable)
For example:
- Fever is the node we’re talking about.
2. “Parent(s)” = the nodes with arrows pointing into it
For example:
- If Disease → Fever,
then Disease is the parent, and Fever is the child.
3. “How likely it is given its parent(s)” means:
What is the probability of this node (like Fever),
depending on the value(s) of its parent(s) (like Disease).
Real example:
| Condition | Probability of Fever |
|---|---|
| Disease = Yes | 0.8 (80%) |
| Disease = No | 0.1 (10%) |
This table says:
- If the person has the disease, they have an 80% chance of fever
- If the person does not have the disease, they still might have fever, but only 10% chance
Why it’s called Conditional Probability:
Because the probability of Fever is conditional on (depends on) whether Disease is Yes or No.
That’s why it’s stored in a Conditional Probability Table (CPT) for each node.
Summary:
| Phrase | Meaning |
|---|---|
| “How likely it is” | The probability of a variable (like Fever) |
| “Given its parent(s)” | Based on the values of variables it depends on (like Disease) |
| Example | P(Fever = Yes |
- Example:
- If Disease = Yes, then P(Fever = Yes) might be 0.8
- If Disease = No, then P(Fever = Yes) might be 0.1
3. Bayes’ Theorem:
The network updates beliefs when new information is received using Bayes’ Theorem:
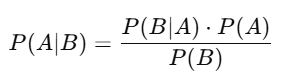
Original sentence:
“The network updates beliefs when new information is received using Bayes’ Theorem:”
What does it mean?
“The network”
This refers to the Bayesian Network, which is a model made of nodes (variables) and arrows (relationships).
“Updates beliefs”
- Beliefs = what the network currently thinks is likely (probabilities).
- To update beliefs means to change or adjust those probabilities based on new evidence.
Consider it as follows:
“I’ll revise my belief now that I have new information.”
“When new information is received”
This means you observe or learn something new — like:
- The patient does have a fever
- The email contains the word “free”
- The machine is making a strange sound
That new evidence helps the network make better guesses about other things.
“Using Bayes’ Theorem”
This is a mathematical rule that tells you how to adjust your probabilities after getting new evidence.
Bayes’ Theorem:
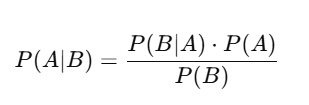
This tells you:
How likely A is after observing B.
What does this mean?
“How likely A is after seeing B”
Let us dissect it in detail:
In Bayes’ Theorem:
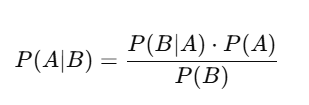
This formula calculates:
Given that we know that B has occurred, what is the likelihood that A will occur?
What do A and B represent?
- A = The topic of your inquiry (e.g., Does the patient have a disease?)
- B = The fresh evidence you just noticed, such as the patient’s fever
So the phrase:
“How likely A is after observing B”
Means:
What’s the chance that A is true, given that we now know B is true?
Real Example:
- A = Person has the flu
- B = Person has a fever
We want to know:
P(Flu | Fever) → What’s the chance a person has flu if we see that they have a fever?
This is different from just knowing:
- P(Flu) → How common flu is in general
- P(Fever | Flu) → How likely fever is if someone has flu
How to read this:
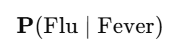
As you read it:
“The probability of Flu given Fever”
Or more naturally:
“If we are aware that someone has a fever, the likelihood that they have the flu.”
What each part means:
| Part | Meaning |
|---|---|
| P(…) | “Probability of…” (how likely something is) |
| Flu | The thing you’re trying to find the probability of |
| ** | ** (vertical bar) |
| Fever | The evidence or observed fact |
Why it matters:
This is conditional probability:
You’re not asking, “What is the chance of flu in general?”
You’re asking, “What is the chance of flu knowing the person has a fever?”
Summary:
| Symbol | Spoken as | Meaning |
|---|---|---|
| P(Flu) | “Probability of Flu” | How common flu is in general |
| **P(Flu | Fever)** | “Probability of Flu given Fever” |
Summary:
| Term | Meaning |
|---|---|
| “How likely A is” | The probability that A is true |
| “After observing B” | Once we have seen or learned that B is true (new evidence) |
| Full meaning | What is the probability that A is true based on the evidence B |
Example:
- You want to know: P(Disease | Fever) = How likely is disease if a person has a fever?
Using Bayes’ Theorem:
- You already know:
- P(Fever | Disease) → How often fever happens in disease
- P(Disease) → How common the disease is
- P(Fever) → How common fever is in general
→ You use these values to update your belief about disease after seeing fever.
Summary:
| Phrase | Meaning |
|---|---|
| Updates beliefs | Changes probabilities based on new evidence |
| New information is received | You observe or learn something (like symptoms, results, etc.) |
| Using Bayes’ Theorem | Applying a math rule to recalculate what’s most likely |
This allows the network to infer new probabilities based on evidence.
Example: Medical Diagnosis
Suppose you have a network for disease diagnosis:
- Nodes:
- Disease (D)
- Fever (F)
- Test Result (T)
- You know:
- P(Fever | Disease) = High
- P(Test Positive | Disease) = High
- Now, a patient has Fever and a Positive Test.
→ The network updates the belief:
P(Disease | Fever, Positive Test) becomes high.- Sentence:
“P(Disease | Fever, Positive Test) becomes high.”
What does it mean?
This is a conditional probability:
P(Disease ∣ Fever, Positive Test) Read as:
“The probability of the disease, given that the patient has a fever and a positive test result.”
What is it saying?
When both Fever and a Positive Test are observed:
The Bayesian Network uses that evidence to update its belief.
It now thinks:
“Hmm, both signs suggest disease, so the chance (probability) of disease is now high.”
Even though you haven’t confirmed the disease, the model says:
“There’s a strong reason to believe the person has it.”
Analogy:
Imagine:
Fever alone = Maybe the flu (60% chance)
Fever + Positive Lab Test = Strong evidence → Now 90% chance
That updated value:
P(Disease ∣ Fever, Positive Test) = High- 1. What does “Fever alone” mean?
“Fever alone” means the person only has a fever — we have no other evidence yet (like test results).
In this situation, we are only using one symptom (fever) to guess if they have the disease.
Example:
The person has a fever, but no test result yet.
Given that single symptom, we could state:
“They have a 60% chance of having the illness, like the flu.”
This 60% is not certain, but it’s a reasonable guess based on only fever.
2. What does “Now 90% chance” mean? 90% chance of what?
It means there is now a 90% chance the person has the disease, after seeing more evidence.
Specifically:
The person has a fever and a positive lab test.
This combined evidence makes it much more likely they really have the disease.
So the probability becomes:
P(Disease ∣ Fever, Positive Test) = 90%
Recap of the analogy:
Evidence Available
Probability of Disease
Fever alone
60%
Fever + Positive Test
90%
Summary:
“Fever alone” = Only one symptom → Medium chance (e.g., 60%)
“Now 90% chance” = After more evidence → Higher chance of disease
- 1. What does “Fever alone” mean?
- Sentence:
So, even if the disease isn’t confirmed, the probability increases based on evidence.
Use Cases:
| Use Case | Explanation |
|---|---|
| Medical Diagnosis | To predict disease based on symptoms and test results. |
| Spam Filtering | To decide if an email is spam based on keywords, links, and sender behavior. |
| Fault Detection | In machines, if smoke is observed, what’s the probability a motor is overheating? |
| Decision-Making in Robotics | Robots use Bayesian reasoning to decide what to do in uncertain environments. |
Summary:
- Bayesian Networks are used when things are uncertain, but probabilities and relationships between variables are known.
- They support the use of logic and evidence in decision-making and inference.
- Powerful tool in AI for solving real-world uncertain problems.
