Iteration and Recursion in Data Structure – Iteration and Recursion Difference – Coding With Clicks

🔁 Iteration

Definition: Iteration is the process of repeatedly executing a set of instructions using loops like for, while, or do-while.

✅ Key Points:

• Uses loops.
• Repeats until a condition is false.
• Generally more memory efficient because it doesn’t use the call stack.
• Easier to trace/debug in simple scenarios.

🧠 Example:

Let’s calculate factorial using iteration:

#include <iostream>
using namespace std;

int factorial(int n) 
{
    int result = 1;
    for (int i = 2; i <= n; i++) 
   {
        result *= i;
    }
    return result;
}

int main() 
{
    int n = 5;
    cout << "Factorial of " << n << " is: " << factorial(n);
    return 0;
}

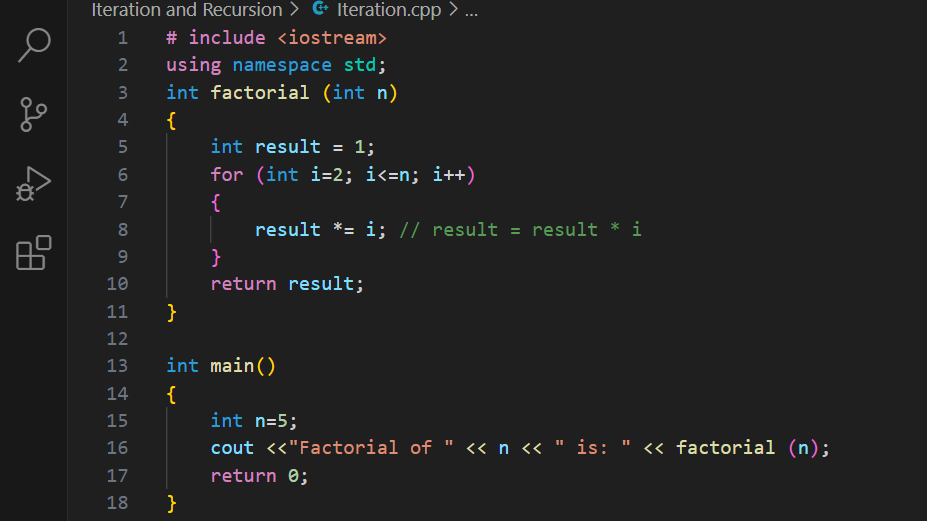
The operator *= is called a compound assignment operator (also known as a short-hand assignment operator).

🧠 What it does:

It multiplies the right-hand side (i) with the left-hand side (result) and then assigns the result back to the left-hand side.

🔁 Recursion

Definition: Recursion is a process where a function calls itself to solve a smaller instance of the same problem.

✅ Key Points:

• Uses function calls.
• Solves problems by breaking them down into smaller sub-problems.
• Uses the call stack, which can lead to stack overflow for large inputs.
• Elegant and concise for problems like tree traversal, Fibonacci, etc.

🧠 Example:

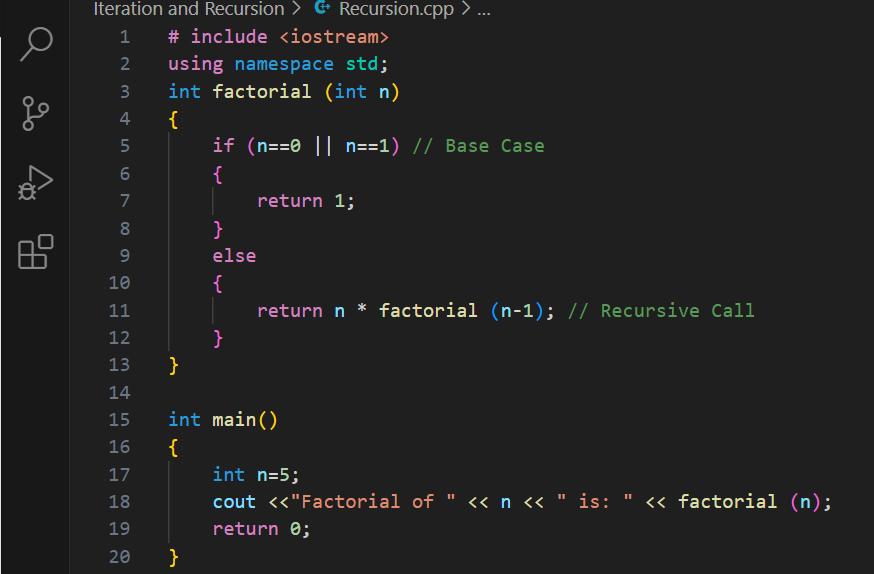
Let’s calculate factorial using recursion:

Now, let’s calculate the same factorial using recursion:

#include <iostream>
using namespace std;

int factorial(int n) 
{
    if (n == 0 || n == 1)  // Base case
        return 1;
    else
        return n * factorial(n - 1);  // Recursive call
}

int main() 
{
    int n = 5;
    cout << "Factorial of " << n << " is: " << factorial(n);
    return 0;
}

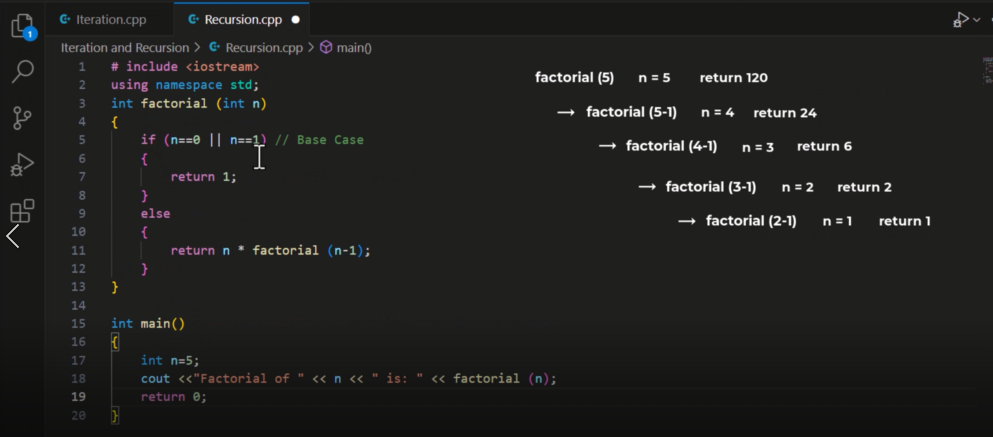
📦 What is the Call Stack?

The call stack is a special memory area used by your program to keep track of function calls.

Every time a function is called (including recursive calls), a stack frame is added to the call stack. This stack frame stores:

• The function’s parameters
• Local variables
• The return address (where to go after the function finishes)

🔁 Why Recursion Uses the Call Stack

In recursion, a function calls itself many times — and each call waits for the next one to finish.

So:

• Each recursive call adds a new stack frame
• These frames build up in memory
• When the base case is reached, the calls return in reverse order, and each stack frame is removed

⚠️ Stack Overflow

If the recursion goes too deep or never ends (no base case), the stack overflows:

💥 This will cause a stack overflow error because the call stack runs out of memory.

📦 Stack = Last In, First Out (LIFO)

Just like stacking plates:

• The last function called is the first one to finish.
• When a function ends, its frame is popped from the stack.

🔄 Comparison:

Feature	Iteration	Recursion
Approach	Loop-based	Function-based (calls itself)
Speed	Usually faster	Can be slower (call overhead)
Memory usage	Low (no stack frames)	High (uses call stack)
Simplicity	Simpler for loops	Simpler for divide-and-conquer
Examples	Searching, sorting loops	Tree traversal, DFS, factorial

🛑 Summary:

• Iteration = more memory-efficient in most cases ✅
• Recursion = elegant for some problems, but heavier on memory ❌ (especially deep recursion)